破解数学难题，计算公式绝技新解大揭秘

　　在数学的世界里，每一个公式都如同一位智者，蕴藏着无尽的智慧。然而，传统的计算方法往往繁琐复杂，让人望而生畏。今天，就让我们一起来探索一些计算公式的新解，这些新解不仅能够简化计算过程，还能让我们对数学有更深的理解。

　　首先，让我们来看一个常见的数学问题：求一个数的平方。传统的方法是使用乘法，即(a^2 = a \times a)。然而，这种方法在处理大数时显得尤为繁琐。现在，我们介绍一种更简便的方法：利用公式(a^2 = (a + b)(a - b) + b^2)。这里，(b)可以是任意一个与(a)无关的数。例如，如果我们要求(123456^2)，我们可以取(b = 1)，那么(123456^2 = (123456 + 1)(123456 - 1) + 1^2 = 152415232 + 1 = 152415233)。这种方法不仅计算速度快，而且易于记忆。

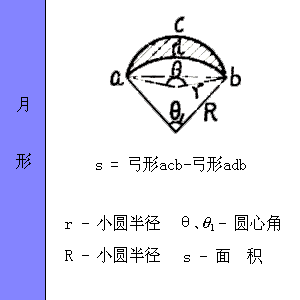
　　接下来，我们来探讨一个有趣的几何问题：求圆的面积。传统的公式是(A = \pi r^2)，其中(r)是圆的半径。但是，如果我们不直接使用(\pi)，而是利用一些巧妙的变换，可以得到一个新的计算方法。例如，我们可以将圆的面积与正方形的面积联系起来，利用公式(A = \frac{4}{\pi} \times (\text{对角线长度})^2)。这里，对角线长度可以通过勾股定理求得。例如，一个半径为(r)的圆，其对角线长度为(2r\sqrt{2})，那么圆的面积(A = \frac{4}{\pi} \times (2r\sqrt{2})^2 = \frac{16r^2}{\pi} \times 2 = \frac{32r^2}{\pi})。这种方法巧妙地避开了直接使用(\pi)，使得计算更加灵活。

　　在代数领域，解一元二次方程也是一个常见的难题。传统的方法是使用求根公式(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a})。然而，这种方法在处理一些特殊情况下会变得复杂。现在，我们介绍一种新的解法：利用配方法。对于一元二次方程(ax^2 + bx + c = 0)，我们可以将其转化为((x + \frac{b}{2a})^2 = \frac{b^2 - 4ac}{4a^2})。这样，我们只需要求出(\frac{b^2 - 4ac}{4a^2})的平方根，然后减去(\frac{b}{2a})，即可得到方程的解。例如，对于方程(x^2 - 6x + 9 = 0)，我们可以将其转化为((x - 3)^2 = 0)，因此(x = 3)。

　　最后，让我们来探讨一个概率问题：从一个装有红球和白球的袋子中随机抽取一个球，求抽到红球的概率。传统的方法是使用条件概率公式(P(A|B) = \frac{P(A \cap B)}{P(B)})。然而，如果我们不直接使用条件概率，而是利用排列组合的方法，可以得到一个新的计算方法。假设袋子里有(n)个球，其中(m)个是红球，那么抽到红球的概率(P(\text{红球}) = \frac{m}{n})。这种方法简单直观，易于理解。

　　总之，通过这些计算公式的新解，我们不仅能够简化计算过程，还能提高解题的效率。在数学的学习和研究中，不断地探索和创新是至关重要的。让我们一起迎接数学世界的挑战，用新的视角去发现那些隐藏在公式背后的智慧吧！